Pole siłowe to nieskończone możliwości dla twórczej ekspresji programisty/grafika. Eksperymentuję z symulacją cząstek i prostym odwzorowaniem wektorów pola w grafikę.

Wykorzystanie pola siłowego

W jaki sposób można wykorzystać pole siłowe w grafice? Standardowo istnieją dwa sposoby:

• symulacja ruchu cząstek podróżujących po “liniach pola”, a następnie rysowanie po tych “liniach” pociągnięciami wirtualnego “pędzla”, który może - na przykład - zmieniać grubość linii w zależności od wartości prędkości cząstki
• rysowanie wewnątrz każdego “oka” siatki jakiejś małej figury bądź kształtu zależnego od wartości wektora pola

Każdemu z tych sposobów warto przyjrzę się teraz bliżej.

Symulacja

Utworzenie cząstek

Najpierw stworzę “cząstki”, czyli zadeklaruję tablicę do przechowywania obiektów klasy Particle i zainicjuję ją pewną - konfigurowalną - liczbą cząstek. Cząstki te posiadają pewne położenie początkowe oraz prędkość początkową (równą zero), a ruch cząstek symulowany jest przez przeliczenie położenia cząstek w każdym cyklu.

Tworząc cząstki, podejmujemy przy okazji decyzję dotyczącą ilości cząstek na początku symulacji:

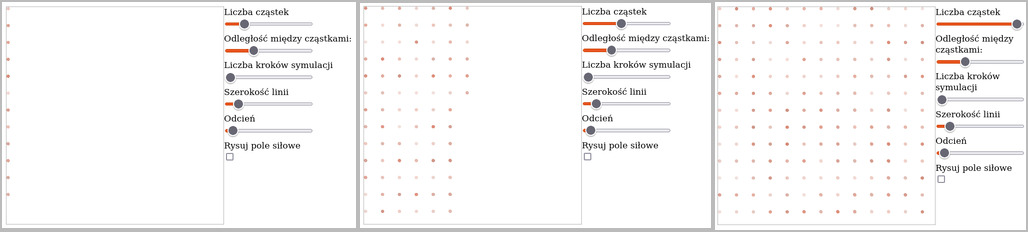
Cząstki mogą się również różnić odlełościami między sobą:

Generatory

Generując położenia cząstek eksperymentuję z różnymi generatorami (w przykładach w tym wpisie używam gridv):

• centered wygeneruje wektor położenia dla cząstki na środku ekranu
• randomv będzie generował nieskończony ciąg wektorów
• gridv rozmieści cząstki na regularnej siatce w odległości space od siebie

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

function *centered() {
  yield createVector(width/2, height/2)
}

function *randomv() {
  while (true) {
    yield(createVector(random(width), random(height)))
  }
}

function *gridv(space) {
  for (let x = s.grid.leftx; x < s.grid.rightx; x+= space) {
    for (let y = s.grid.topy; y < s.grid.boty; y+= space) {
      let v = createVector(x, y)
      yield (v)
    }
  }
}

Zbiór cząstek reprezentuję jako obiekt klasy Particles, który w konstruktorze otrzymuje generator położeń:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Particles {
  constructor(n, vecGen) {
    this.ps = []
    for (let i = 0; i < n; i++) {
      let nv = vecGen.next()
      if (!nv.done) {
        this.ps.push(new Particle(nv.value))
      }
    }
  }

  accellerate(grid) {
    this.ps.map(p => p.accellerate(grid))
  }

  update() {
    this.ps.map(p => p.update())
  }

  draw() {
    push()
    this.ps.map(p => p.draw())
    pop()
  }

}

Wędrówka cząstek

Jak przebiega taka symulacja? W każdym cyklu symulacji muszę policzyć:

• jakie jest przyspieszenie cząstki (założę, że jest równe sile działającej na cząstkę w jej obecnym położeniu)
• jaka jest wynikająca z tego przyspieszenia prędkość (należy zwiększyć prędkość o wartość przyspieszenia)
• oraz jakie będzie położenie cząstki na początku kolejnego cyklu (czyli dodać wartość prędkości do położenia)

Każde kolejne położenie należy jakoś (ha!) graficznie połączyć z poprzednim położeniem i w ten sposób można łatwo narysować ruch cząstek przez pole siłowe.

Główna pętla

Funkcja rysująca - draw w p5js - w pętli będzie wywoływać trzy operacje:

• wyznaczanie przyspieszenia
• aktualizację położeń cząstek oraz
• rysowanie trasy między starym a nowym położeniem cząstek

W poniższym kodzie s reprezentuje stan programu i przechowuje zarówno dane pola siłowego s.grid jak, cząstki s.particles oraz stan kontrolek s.state:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

function draw() {
  let {particlesCount, particlesDistance, simulationSteps} = s.state
  s.particles = new Particles(particlesCount.value(), gridv(particlesDistance.value()))
  background(s.bg)
  drawGrid()
  for (let i = 0; i < simulationSteps.value(); i++) {
    s.particles.accellerate(s.grid)
    s.particles.update()
    s.particles.draw()
  }
  drawFrame()
}

Rysowanie

Sama symulacja cząstek i obliczanie ich kolejnych położeń to inżynieria. Teraz czas na sztukę. Warto się zastanowić:

• co rysujemy w kolejnych położeniach (kolejne segmenty łamanej, punkty, koła, łuki?)
• jakim rysujemy kolorem, jaką grubością “pędzla”
• czy zmieniamy atrybuty (kolor/grubość) pędzla oraz sposób ysowania podczas przemierzania toru jednej cząstki
• jak na ostateczny rezultat wpłynie początkowy wybór ilości oraz położeń początkowych cząstek

Przykłady

Oto przykłady dla różnych szerokości “pędzla” (przy lekko zrandomizowanej jasności i nasyceniu wybranej barwy) (patrz b3ba345):

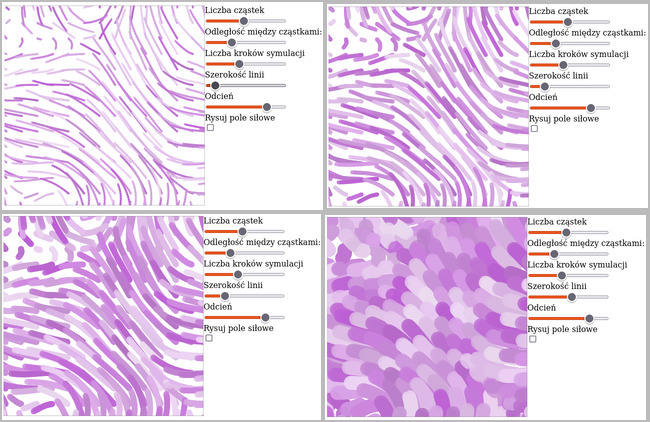
Poniżej przykłady, w którch dla każdej cząstki rysuję wielokąt, którego wierzchołki składają się z kolejnych punktów, przez które przechodzi cząstka podczas symulacji oraz punktów przesuniętych względem nich o wartość “szerokości linii” (patrz 19633fa):

Wykorzystanie wartości pola

Warto zauważyć, że do uzyskania interesujących efektów graficznych wystarczą jedynie wartości samych wektorów pola. Na płótnie można takie wektory zareprezentować na wiele sposobów:

• można wykorzystać współrzędne wektora do ustalenia odcienia i/lub jasności prostokąta będącego “okiem” siatki pola
• można rysować nachylone pod kątem wskazanym przez wektor linie
• można rysować koła/łuki o promieniach ustalonych przez wektor

Możliwości jest bardzo dużo.

Oto przykłady (patrz 1c2b1ce):

Dobór parametrów

Ważny jest również staranny dobór parametrów: ziaren losowości, palet kolorów, położeń początkowych, współczynników kroku dla funkcji noise. Zwykle najwięcej czasu zajmuje określenie odpowiedniego zestawu ich wartości.

Małe zmiany na wejściu mogą spowodować zupełnie inny rezultat wyjściowy i często jedynie eksperymentowanie pozwala w ogóle zorientować się w charakterze powstającego “dzieła”, zrozumieć prawidłowości pomiędzy zmianą parametrów a poziomem estetycznej satysfakcji, jakiej doświadczamy oglądając to, co właśnie tworzymy.

Eksperymentowanie

Jak eksperymentować z prorgamem? Dobrze jest sparametryzować wszystkie wartości, które mają wpływ na ostateczny kształt dzieła i które chcemy często zmieniać po to, żeby sprawdzić, jaki będzie rezultat, na przykład:

• wielkość płótna (wysokość i szerokość)
• wymiary “oka siatki”
• ziarno inicjujące generator liczb losowych oraz generator szumu (noise())
• kolory/odcienie początkowe
• ilość symulowanych cząstek

Określony zestaw wartości, który daje interesujący wynik (czytaj: ciekawą grafikę) warto móc jakoś zapisać. Dobrze by było, gdyby zapisany zestaw wartości mógł również posłużyć do odtworzenia grafiki w dokładnie takiej samej postaci, jak w momencie zapisywania.

Powtarzalność

Tego typu powtarzalność sprawia, że mamy swoje dzieło pod absolutną kontrolą. Przyznam, że zwykle tego nie robię, i zawsze gorzko tego żałuję: umykają mi ciekawe konstelacje barw, intrygujące kształty, wymyślne linie. Jeśli nawet uda mi się zrobić screenshota, to przecież bez wartości początkowych prawdopodobnie już nigdy nie uzyskam dokładnie tego samego efektu.

A bardzo warto zadbać o to, żeby wszelkie “ruchome” czy raczej “zmienialne” parametry wystawiamy jako kontrolki do sterowania na zewnątrz kodu. Biblioteka p5js ma zestaw prostych wraperów na obiekty DOM, dzięki którym można pokusić się o stworzenie “panelu nawigacyjnego”, dzięki któremu będzie można trochę posterować sposobem generowania grafiki.

Źródła

Kod wrzuciłam do projektu snowflake na GitLabie (wersja live).

Ten wpis jest częścią serii strengthfield.

• 2021-11-08 - Wykorzystanie pola siłowego
• 2021-08-08 - Moje małe pole siłowe